Cristian Silva-Perez

Cristian Silva-Perez

PhD candidate

Near-real time monitoring system: Brief overview to Gaussian process state space models GPSS

4 minute read

Published:

This blog post presents a brief introduction to Gaussian Process State Space models (GPSS) and how it can be used as a near-real time monitoring framework. The framework is shown in the figure below where each of the blocks is numbered to facilitate following the sequence of operations. Our purpose is to estimate in real time as new observations arrive, the D-dimensional system state denoted by the random vector xk (block 10), where k represents the time index in which the system is at, and the D dimensions are defined by the D number of system state variables assumed to characterise the system state.

Start (block 1)

The monitoring algorithm starts from the latest system state obtained in block 10. This is, the system state estimated at time k is fed back to begin a new estimation becoming then the state at k-1.

img

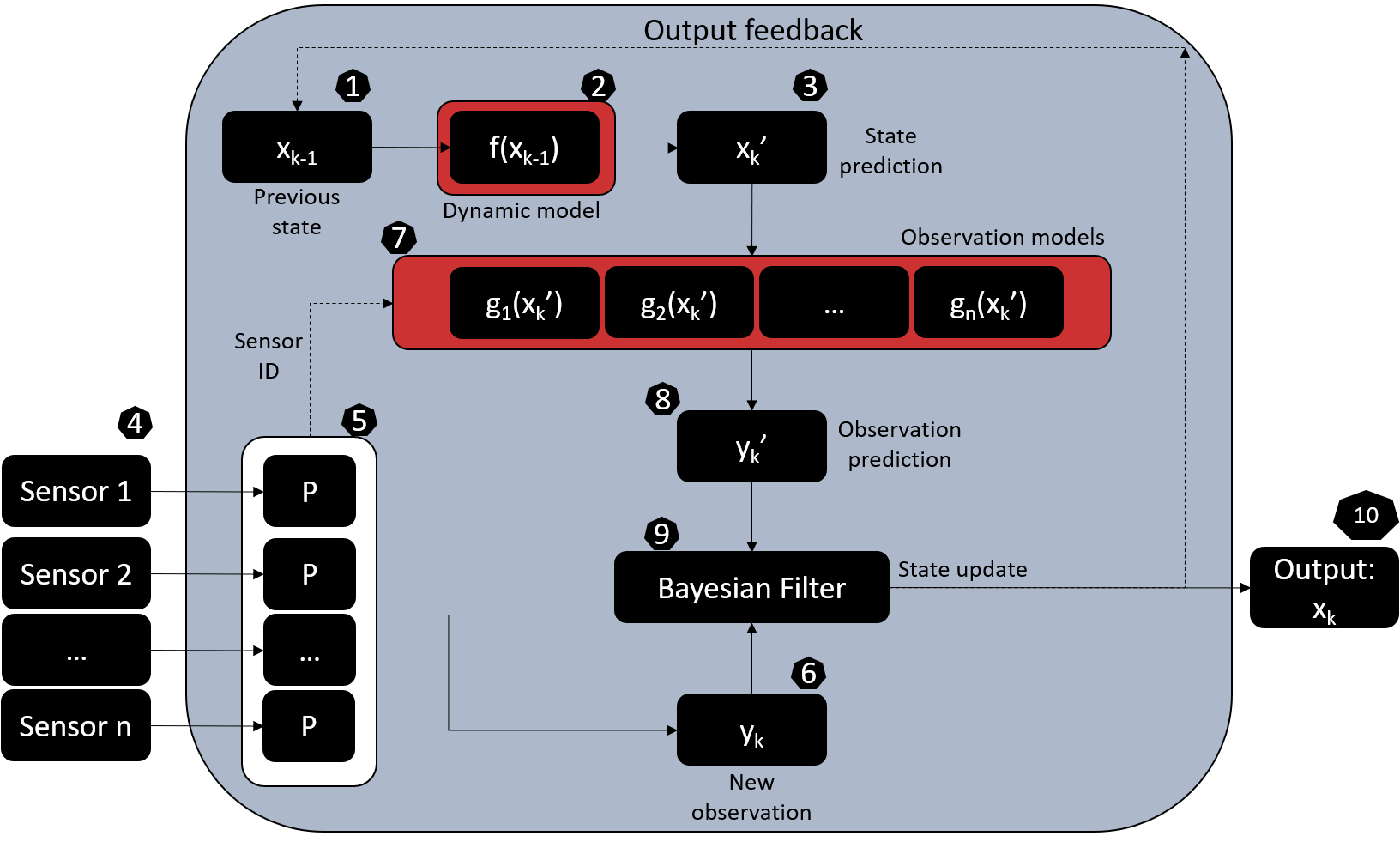
Dynamic model and state prediction (Blocks 2 and 3)

The dynamics of evolution of the state variables are represented by the probabilistic transition model specified by:

xk = f(xk-1) + qk (1)

In equation (1) the system state at a given date k can be estimated as a function of the previous state xk-1 using the non-linear function f(.) and considering the additive gaussian system noise qk – N (0, Qk) accounting for the model uncertainty when making predictions. Note that the non-linear function f(.) represents the evolution rule of the dynamical system, which is a function that describes what future states follow from the current state. This can be seen as a stochastic differential equation and be learned by approximating it with a Gaussian process regression as proposed here. A future post will present the python code to implement this operation. Note that the transition model of equation (1) results in the conditional probability distribution P (xk | xk-1). In the blocks 3 and 4 the state is represented with the vector xk’ since it is not yet the estimated current state but our prediction of it based on the previous state.

Observation pre-processing and feature extraction (blocks 4 to 6)

When a new observation is available sometimes is required to perform a pre-processing step on the sensor measurements to adequate them to enter the monitoring system. It can also be beneficial to extract other informative features that may on their own have an associated algorithm (Block P). Also note that in this step the sensor ID is extracted and transmitted to block 7.

New vector of observations ready (Block 6)

After pre-processing the raw sensor measurements the system observables are ready to be introduced in the tracking algorithm (Block 9).

Observations prediction (Blocks 7 and 8)

The E-dimensional random vector of sensor observations yk can be predicted as a function of the system state xk by means of the observation model:

yk = g(xk) + rk (2)
Where the E dimensions correspond to the number of sensor observables, g(.) is a non- linear function mapping from system state to remote sensing observations and rk – N (0, Rk) is the additive gaussian measurement noise accounting for noise effects associated to the sensors. Note that block 7 receives the sensor ID from block 5 and the observation model associated to this sensor is used to make the prediction. This is one of the methods how sensors with asynchronous temporal resolution can be combined in the same monitoring process. Also note that the observation probabilistic model of equation (2) results in the condition probability distribution P (yk | xk) describing the likelihood of getting the observations yk given the state xk.

State update

In order to achieve near-real time monitoring a Bayesian Filtering Framework (BFF) is used under which after every new observation at time k, we update our belief of the hidden system state xk considering from the first to the latest available observations acquired so far (y1:k) (assuming Markov property), regardless of the sensor that provides the acquisition. This belief is represented by the posterior probability distribution P(xk | y1:k) which in a BFF is estimated by recursively solving the prediction and update Bayesian filtering equations. Depending on the assumptions regarding the state distribution and the way of solving the Bayesian equations, the filter can become a non-linear Kalman filter or a Particle filter (a sequential Monte Carlo based sampling technique).

Output

After obtaining an estimation of the system state, this operation can be applied at a pixel level to obtain maps, at object level seeing the problem as a time series or signal processing filter, to obtain the desired final outputs. The result is the fed back to block 1 to restart the recursive estimation process.